3.1 The PackedTable class
3.1.1. The PackedTable class and subclasses
The PackedTable class is very flexible and is meant to facilitate the ordering, the slicing and the MPI-distribution of a set of elements with associated properties. Such elements can be for instance map pixels, time samples with associated astrometry or detectors of given geometries and characteristics. An Acquisition instance will have at least 3 PackedTable attributes:
sceneinstrument.detectorsampling
The first one holds the shape of the acquisition’s input scene.shape and the other two the shape of the acquisition’s output (len(instrument.detector), len(sampling). Here are examples of PackedTable subclasses:
|
LayoutGrid | Rectangular layout ||
LayoutGridCircles | Rectangular layout of circles ||
LayoutGridSquares | Rectangular layout of squares ||
Sampling | Temporal layout ||
PointingEquatorial | Temporal layout with equatorial coordinates ||
PointingHorizontal | Temporal layout with horizontal coordinates |
The following snippet creates a grid of square detectors:
>>> spacing = 0.001
>>> layout = LayoutGridSquares((16, 16), spacing, filling_factor=0.8)
>>> layout.plot()
And this one, a grid of circles:
>>> layout = LayoutGridCircles((16, 16), spacing)
>>> layout.plot()
More generally, it is possible to specify the positions by hand:
>>> center = [[[-1.5, 1.5], [0, 1], [1.5, 1.5]],
[[-1, 0 ], [0, 0], [1, 0 ]],
[[-1.5, -1.5], [0, -1], [1.5, -1.5]]]
>>> layout = Layout((3, 3), center=center)
>>> layout.plot()
3.1.2. The packed and unpacked mirroring
A PackedTable instance stores information about its components, such as the spatial location or any property.
During a PackedTable instanciation, some components may be discarded by using the selection keyword, either because the components do not physically exist, or because they are not handled by the processing node if the work is distributed and executed in parallel. The components can also be ordered through the ordering keyword.
In most cases, it is more convenient to travel the component characteristics in a 1-dimensional ordered array (the packed array, which does not contain the removed components), but in some other cases, it is more practical to access them through a multi-dimensional array mimicking the multi-dimensional layout (the unpacked array, which includes the removed components and those handled by other processes). One purpose of the PackedTable class is to make these two access patterns transparent by mirroring them through special attributes that can be returned as packed or unpacked arrays. The special attributes are those that are passed as keywords in the PackedTable instanciation. Although only unpacked arrays can be passed during the instanciation, the PackedTable instance only stores for efficiency reasons the packed values, which are accessed as regular attributes. The mirrored unpacked values are then accessed through the all attribute.
>>> shape = (3, 3)
>>> spacing = 1.
>>> selection=[[True, True, False ],
[True, True, True],
[True, True, True]]
>>> gain = [[1.0, 1.2, 1.5],
[0.9, 1.0, 1.0],
[0.8, 1.0, 1.0]]
>>> detectors = LayoutGridSquares(shape, spacing, selection=selection,
gain=gain)
>>> detectors.shape
(3, 3)
>>> len(detectors)
8
>>> len(detectors.all)
9
>>> detectors.all.removed
array([[False, False, True],
[False, False, False],
[False, False, False]], dtype=bool)
>>> detectors.gain
array([ 1. , 1.2, 0.9, 1. , 1. , 0.8, 1. , 1. ])
>>> detectors.all.gain
array([[ 1. , 1.2, nan],
[ 0.9, 1. , 1. ],
[ 0.8, 1. , 1. ]])
>>> detectors.center.shape, detectors.all.center.shape
((8, 2), (3, 3, 2)
>>> detectors.vertex.shape, detectors.all.vertex.shape
((8, 4, 2), (3, 3, 4, 2)Any external unpacked array can be packed:
>>> values = np.arange(9).reshape(shape)
>>> detectors.pack(values)
array([0, 1, 3, 4, 5, 6, 7, 8])And conversely, any packed array can be unpacked. By default, for removed components, -1 is used for integer arrays and NaN otherwise, but this value can be specified with the missing_value keyword.
>>> detectors.unpack(np.arange(8))
array([[ 0, 1, -1],
[ 2, 3, 4],
[ 5, 6, 7]])
>>> detectors.unpack(np.arange(8, dtype=float) * 2)
array([[ 0., 2., nan],
[ 4., 6., 8.],
[ 10., 12., 14.]])3.1.3. Component ordering
In the previous examples, the ordering of the packed components follows the row-major storage of the unpacked arrays. This default ordering can be modified to follow a more appropriate numbering scheme. Let’s consider a detector array made of 4 identical subarrays. Because cross-talk will most likely affect detectors of the same subarray, and assuming that each subarray has its own readout electronic system, detectors in each subarray will have common artifacts, and it will be interesting to group them in the packed arrays. The new numbering of detectors is specified through the ordering keyword.
>>> a = arange(16).reshape((4, 4))
>>> ordering = np.vstack([np.hstack([a, a + 16]),
np.hstack([a + 32, a + 48])])
>>> detectors = LayoutGridSquares((8, 8), 0.250, ordering=ordering)
>>> detectors.plot()
>>> for (x, y), s in zip(detectors.center, np.arange(len(detectors))):
>>> text(x, y, s, horizontalalignment='center', verticalalignment='center')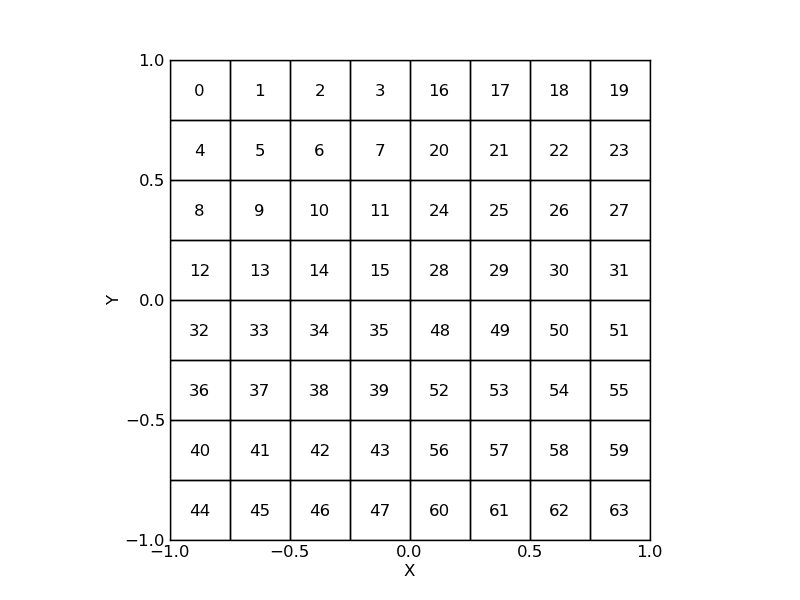
The packed components are sorted according to their ranks in the ordering array. By specifying a negative value, it is possible to remove a component not already discarded by the selection keyword. The correspondance between packed and unpacked elements relies on the special index attribute, which is derived from the input selection and ordering keywords. It stores the unpacked row-major 1-dimensional indices of the packed components.
>>> detectors.index
array([ 0, 1, 2, 3, 8, 9, 10, 11, 16, 17, 18, 19, 24, 25, 26, 27, 4,
5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, 29, 30, 31, 32, 33,
34, 35, 40, 41, 42, 43, 48, 49, 50, 51, 56, 57, 58, 59, 36, 37, 38,
39, 44, 45, 46, 47, 52, 53, 54, 55, 60, 61, 62, 63])3.1.4. PackedTable slicing and splitting
A PackedTable instance can be sliced and iterated over:
>>> samples = Sampling(100, angle=np.arange(100) * 360 / 100)
>>> len(samples[:10]), len(samples[:10].all)
(10, 100)
>>> samples[:10].angle
array([ 0. , 3.6, 7.2, 10.8, 14.4, 18. , 21.6, 25.2, 28.8, 32.4])
>>> for s in samples:
... print(s.angle)It can also be split into a number of sections with approximately the same size:
>>> samples = Sampling(100, angle=np.arange(100) * 360 / 100)
>>> groups = samples.split(3)
>>> [len(_) for _ in groups]
[34, 33, 33]3.1.5. PackedTable MPI-scattering
During the execution of an MPI job, a PackedTable instance can be MPI-scattered, i.e. distributed to a set of MPI processes. Accessing the unpacked attributes through the all attribute or calling the method unpack will MPI-gather the local arrays into a global one.
In the following example, the property angle1 will be set globally and the other property angle2 locally. Given the file:
# file test_scatter.py
from __future__ import division, print_function
import numpy as np
from mpi4py import MPI
from pysimulators import Sampling
rank = MPI.COMM_WORLD.rank
samples = Sampling(10, angle1=np.arange(10) * 360 / 10, angle2=None)
samples = samples.scatter()
samples.angle2 = rank * 90 + np.arange(len(samples))
print(rank, len(samples), len(samples.angle1), len(samples.angle2))
angle1 = samples.all.angle1
angle2 = samples.all.angle2
if rank == 0:
print(angle1)
print(angle2)Let’s execute it using 3 MPI processes:
$ mpirun -n 3 python test_scatter.py
(1, 3, 3, 3)
(2, 3, 3, 3)
(0, 4, 4, 4)
[ 0. 36. 72. 108. 144. 180. 216. 252. 288. 324.]
[ 0 1 2 3 90 91 92 180 181 182]3.1.6. More on the special attributes
As already mentionned, for memory efficiency, only the packed arrays are stored in memory, which implies the following limitations:
- the component selection and ordering cannot be changed once the layout is created: the
indexattribute is read-only. - modifications of the values contained in an unpacked array are prevented by making the unpacked arrays read-only.
Here is the wrong way to make an assignment:
>>> layout = Layout(10, selection=slice(5, 10), val=np.random.random(10))
>>> layout.all.val[5] = 10
ValueError: assignment destination is read-onlyThis one is correct:
>>> unpacked = layout.all.val.copy()
>>> unpacked[5] = 10
>>> layout.all.val = unpackedbut the following is better, because it avoids copies:
>>> layout.val[0] = 10Special attributes can also be functions, in order to decrease the memory footprint. In this case, the function is called each time the attribute is accessed. For instance, the LayoutGrid class uses such a mechanism for the row and column special attributes to avoid storing them in memory.
These functions must return packed arrays. They can have:
- no argument, by using the parent scope variables. Note that Python’s handling of closure may be unintuitive (to be polite) and is a frequent source of mistakes. It is necessary to check that these parent scope variables are not reassigned to another value after the function is defined, since the new values would be the ones used in the function.
>>> x = [0, 7, 14]
>>> layout = Layout(3, val=lambda: x)
>>> layout.val
[0, 7, 14]- one argument, which is then the layout itself. Continuing the example in the previous section of a
Layoutmade of 4 subarrays, we can define a special attributesubarrayusing a function that will return to which subarray a detector belongs.
>>> a = arange(16).reshape((4, 4))
>>> ordering = np.vstack([np.hstack([a, a + 16]),
np.hstack([a + 32, a + 48])])
>>> def subarray(self):
... i = self.index // 32
... j = (self.index % 8) // 4
... return i * 2 + j + 1
>>> layout = LayoutGridSquares((8, 8), 0.250, ordering=ordering,
subarray=subarray)
>>> layout.plot()
>>> for (x, y), s in zip(layout.center, layout.subarray):
>>> text(x, y, s, horizontalalignment='center', verticalalignment='center')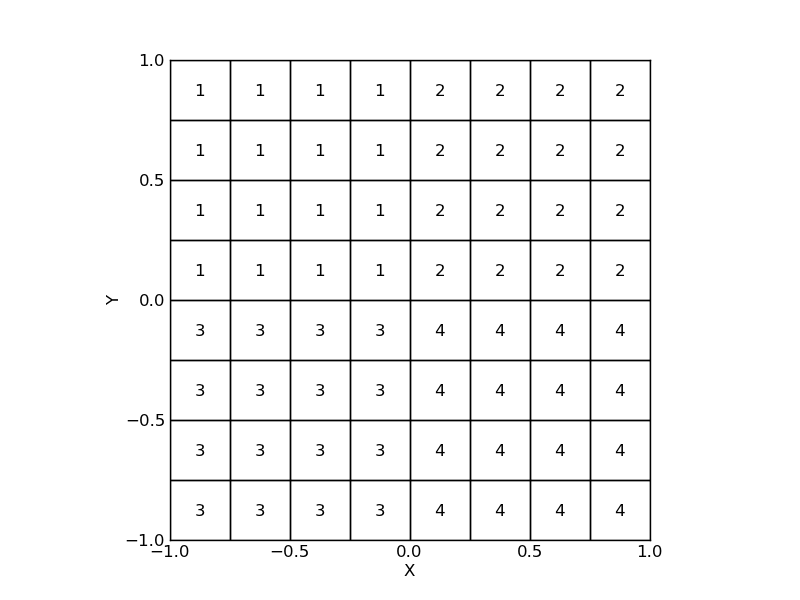
- or more, in which case the special attribute remains a function:
>>> selection = [True, True, True, False]
>>> layout = Layout(4, selection=selection, val=[0, 7, 14, 21], func=lambda s, v: s.val+v)
>>> layout.func(10)
np.array([10, 17, 24])
>>> layout.all.func(10)
np.array([10, 17, 24, -1])A special packed attribute can also be a scalar, in which case only the unpacked mirrored array is dimensional.
